

Convex Hull
Get started
জয় শ্রী রাম
🕉
Prerequisite: Fundamentals of Sweep Line Algorithm
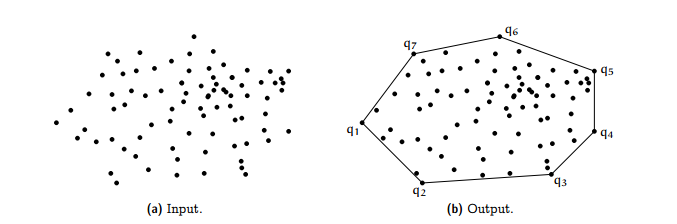
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. Convex means that the polygon has no corner that is bent inwards. If S is a set of points, then convex hull is the smallest convex polygon which covers all the points of S.
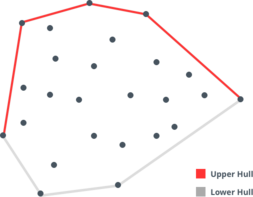
From above diagram it is quite clear that once we look Convex hull as combination of one upper hull and one lower hull, the problem of constructing convex hull for a given set of points naturally becomes a great candidate for Sweep Line algorithm.
If you think enough, you would be able to convince yourself that
- if you sweep a vertical line across the plane either from left to right or from right to left (depending on whether we want to form the convex hull in clockwise manner or counterclockwise), and while doing so if you collect the point (from the given set of points) with the highest y-coordinate at any x-coordinate, you would get the upper portion of convex hull. Let's call it upper hull.
- if you sweep a vertical line across the plane either from right to left or from left to right (depending on whether we want to form the convex hull in clockwise manner or counterclockwise), and while doing so if you collect the point (from the given set of points) with the lowest y-coordinate at any x-coordinate, you would get the lower hull.
Another thing worth noting from the above diagram is that:
-
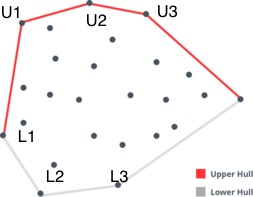
Take any ordered set of 3 consecutive points on the UPPER hull from ordered from left to right.
Let's suppose these
3 points are U1, U2 and U3,
U1 being the leftmost point and U3 rightmost. Now let's imagine we have directed edges from U1 to U2, U2 to U3 and U3 to back to U1. For any such points U1, U2, U3 on the upper hull you will notice that the orientation of the cycle U1-> U2 -> U3 -> U1 is CLOCKWISE. Please see the below section on Orientation for more information.
-
Take any ordered set of 3 consecutive points on the LOWER hull from ordered from right to left.
Let's suppose these
3 points are L3, L2 and L1,
p3 being the rightmost point and p1 leftmost. Now let's imagine we have directed edges from L3 to L2, L2 to L1 and L1 to back to L3. For any such points L3, L2, L1 on the lower hull you will notice that the orientation of the cycle L3 -> L2 -> L1 -> L3 is CLOCKWISE.
Orientation:
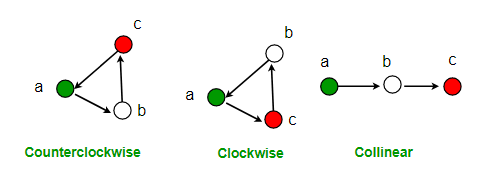
The above picture gives a very clear idea about orientation of three ordered points.
Now, given three ordered points how do we determine their orientation? Answer is by using the concept of Slope. Slope of a straight line P1P2 is the tan of the angle it forms with the X-axis. If coordinates of point P1 is (x1, y1), and that of P2 is (x2, y2), and the angle between P1P2 and X-axis is theta, then
Slope = tan theta = delta Y / delta X = (y2 - y1) / (x2 - x1)
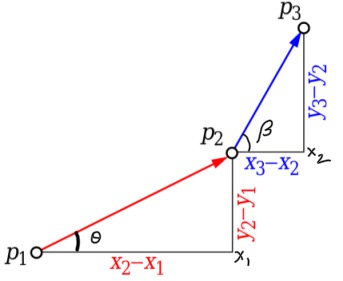
From the above diagram it is very easy to say that:
-
p1p2 and p2p3 will be collinear if and only if:
Angle P3P2X2 (or, angle beta) = Angle P2P1X1 (or, angle theta), i.e.,
(y3 - y2) / (x3 - x2) = (y2 - y1) / (x2 - x1),
or, (y3 - y2) * (x2 - x1) = (y2 - y1) * (x3 - x2) , multiplied each side by (x3 - x2) * (x2 - x1)
or, (y3 - y2) * (x2 - x1) - (y2 - y1) * (x3 - x2) = 0 -
Orientation of p1p2p3 will be clockwise if and only if:
Angle P3P2X2 (or, angle beta) < Angle P2P1X1 (or, angle theta), i.e.,
(y3 - y2) / (x3 - x2) < (y2 - y1) / (x2 - x1),
or, (y3 - y2) * (x2 - x1) < (y2 - y1) * (x3 - x2) , multiplied each side by (x3 - x2) * (x2 - x1)
or, (y3 - y2) * (x2 - x1) - (y2 - y1) * (x3 - x2) < 0 -
Orientation of p1p2p3 will be counterclockwise if and only if:
Angle P3P2X2 (or, angle beta) > Angle P2P1X1 (or, angle theta), i.e.,
(y3 - y2) / (x3 - x2) > (y2 - y1) / (x2 - x1),
or, (y3 - y2) * (x2 - x1) > (y2 - y1) * (x3 - x2) , multiplied each side by (x3 - x2) * (x2 - x1)
or, (y3 - y2) * (x2 - x1) - (y2 - y1) * (x3 - x2) > 0
// Method to find orientation of ordered triplet
// (p1, p2, p3). The function returns
// following values
// zero: p, q and r are colinear
// negative integer: p1 -> p2 -> p3 -> p1 forms Clockwise cycle
// positive integer: p1 -> p2 -> p3 -> p1 forms Counterclockwise cycle
private int direction(int[] p1, int[] p2, int[] p3) {
return ((p2[1] - p1[1]) * (p3[0] - p2[0])) - ((p3[1] - p2[1]) * (p2[0] - p1[0]));
}
So, now that we have knowledge about all the bits and pieces we need to implement the algorithm to compute Convex Hull, let's look at the complete implementation below:
public class ComputationalGeometry {
public int[][] convexHull(int[][] points) {
if (points == null || points.length == 0) {
return new int[0][];
}
// Sort the given points: ascending on x first, then descending on y
//
// reason: We will be creating the overall convex hull
// in clockwise manner.
// so, while building the upper hull,
// if there are more than one points
// at the same x-coordinate, only the point with the
// highest y-coordinate will be in the upper hull.
// so we should have the point with the highest y-coordinate at first
// when there are points with same x-coordinate.
//
// Similarly, while creating the lower hull, which we
// will be creating from right to left (because we
// are creating the overall convex hull in clockwise direction),
// we iterate on the points from right to left, so in this case
// we would get the point with the lowest y-coordinate first for those
// points with same x-coordinate. And this is exactly what we want because
// in lower hull we will include the points with the lowest y-coordinate
// for the points with same x-coordinate.
Arrays.sort(points, (a, b) -> a[0] - b[0] == 0 ? b[1] - a[1] : a[0] - b[0]);
List<int[]> hull = new ArrayList<>(); // EVENTS
// create upper hull from by SWEEPING A VERTICAL LINE left to right
for (int i = 0; i < points.length; i++) {
// delete all the recently added points till the
// remaining hull makes clockwise orientation with
// the current point we are going to add.
while (hull.size() > 1
&& direction(hull.get(hull.size() - 1), hull.get(hull.size() - 2), points[i]) > 0) {
hull.remove(hull.size() - 1);
}
// now that we know the current point will form a clockwise orientation
// with the rest of the points already in the upper hull (after the deletion done above),
// add the current point to the upper hull
hull.add(points[i]);
}
// create lower hull by SWEEPING A VERTICAL LINE
//from right to left across the plane
for (int j = points.length - 1; j >= 0; j--) {
// delete all the recently added points till the
// remaining hull makes clockwise orientation with
// the current point we are going
// to add. (while creating the lower hull from right to left)
while (hull.size() > 1
&& direction(points[j], hull.get(hull.size() - 1), hull.get(hull.size() - 2)) > 0) {
hull.remove(hull.size() - 1);
}
// now that we know the current point will form a clockwise orientation
// with the rest of the points already in the hull (after the deletion done above),
// add the current point to the convex hull already formed hull
hull.add(points[j]);
}
HashSet<int[]> res = new HashSet<>(hull);
return res.toArray(new int[res.size()][]);
}
// To find orientation of ordered triplet
// (p1, p2, p3). The function returns
// following values
// zero --> p, q and r are colinear
// negative integer --> Clockwise
// positive integer --> Counterclockwise
private int direction(int[] p1, int[] p2, int[] p3) {
return ((p2[1] - p1[1]) * (p3[0] - p2[0])) - ((p3[1] - p2[1]) * (p2[0] - p1[0]));
}
}
Related Must-Read Topics:
- 1d Range Search
- Closest Pair
-
Dual Line Sweep
& Rectangles Union -
2D Intervals Union
& Skyline Problem - Overlapping 1D Intervals
- Merging Overlapping 1D Intervals
- Separating Overlapping 1D Intervals
