

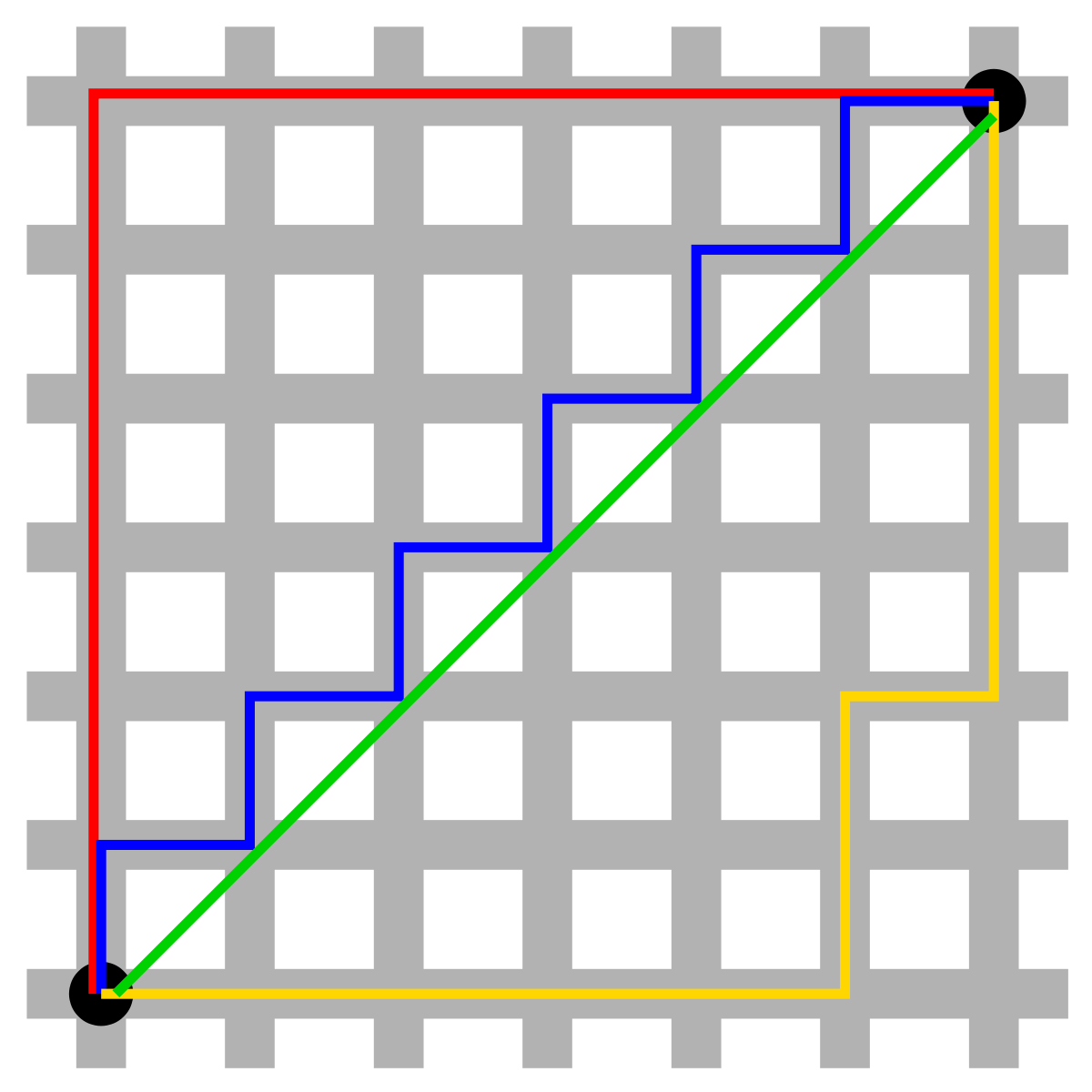
Taxicab Distance
Get started
জয় শ্রী রাম
🕉Let’s suppose we have two points A(x1, y1) and B(x2, y2).
In Euclidean geometry the distance between A and B would be: root of ( (x1 – x2)^2 + (y1 – y2)^2 )
Whereas in Taxicab geometry the distance between A and B would be: |x1 – x2| + |y1 – y2|
Taxicab Distance is also known as Manhattan Distance.
Use Cases:
Some of the scenarios where using Taxicab Distance is appropriate :
1. Where only vertical and horizontal movement is permitted. No other movements are allowed.
2. Only diagonal movements are allowed. No other movement is permitted.
Taxi Drivers – GPS – Cities with only straight roads intersecting each other only at 90 degree
The name Taxicab Geometry gets its name from the fact that it is of immense importance when it comes to measure distances between two points for a taxi driver to travel in a city which has only straight roads intersecting each other only at 90 degree.
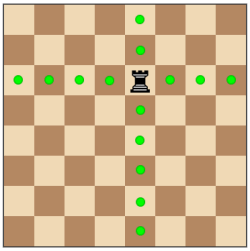
Chess
In Chess, the distance between squares for rooks and bishops are measured using taxicab distance.
The rook can move any number of squares in a straight line along any column or row. They CANNOT move diagonally for any reason.chess1
The bishop may move any number of squares in a diagonal direction until it is prevented from continuing by another piece.

Where Taxicab Distance cannot be used?
Taxicab Distance CANNOT be used in scenarios where :
1. vertical, horizontal and diagonal are all allowed together.
For example, the queen is, without a doubt, the most powerful piece on the chessboard. She can move as many squares as she desires and in any direction (barring any obstructions).

2. there are some restrictions on the movement.
For example, the king can only move one square in any direction (except in the case of the castle maneuver). There is an important restriction on his movement – he may not move into a position where he may be captured by an opposing piece.

Application of Taxicab Distance:
Below is a problem where Taxicab Distance can be appropriately used:
Problem: Escape The Ghosts
You are playing a simplified Pacman game. You start at the point (0, 0), and your destination is (target[0], target[1]). There are several ghosts on the map, the i-th ghost starts at (ghosts[i][0], ghosts[i][1]).
Each turn, you and all ghosts simultaneously *may* move in one of 4 cardinal directions: north, east, west, or south, going from the previous point to a new point 1 unit of distance away.
You escape if and only if you can reach the target before any ghost reaches you (for any given moves the ghosts may take.) If you reach any square (including the target) at the same time as a ghost, it doesn’t count as an escape.
Return True if and only if it is possible to escape.
Example 1: Input: ghosts = [[1, 0], [0, 3]] target = [0, 1] Output: true Explanation: You can directly reach the destination (0, 1) at time 1, while the ghosts located at (1, 0) or (0, 3) have no way to catch up with you. Example 2: Input: ghosts = [[1, 0]] target = [2, 0] Output: false Explanation: You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination. Example 3: Input: ghosts = [[2, 0]] target = [1, 0] Output: false Explanation: The ghost can reach the target at the same time as you.
Solution:
Intuition:
Login to Access Content
Algorithm:
Login to Access Content
Java Code:
Login to Access Content
Python Code:
Login to Access Content
Complexity Analysis:
Please subscribe to access the complexity analysis.
