

Heap Operations
Get started
জয় শ্রী রাম
🕉- Prerequisite for this chapter: Heap Fundamentals
We will be discussing implementation of insertion of a new element and deletion of max element in a Max Heap.
Get Element with Max Value:
GetMax() is easy. The max (for max heap) is the root of the complete binary tree and so happens to be the first element in the array. Just return the element at index 0 in the array for GetMax().
public int getMax() {
return arr[0];
}
Insert a new element:
While implementing insertion of a new element in a Heap, you need to keep in mind that a Heap is a Complete Binary Tree.
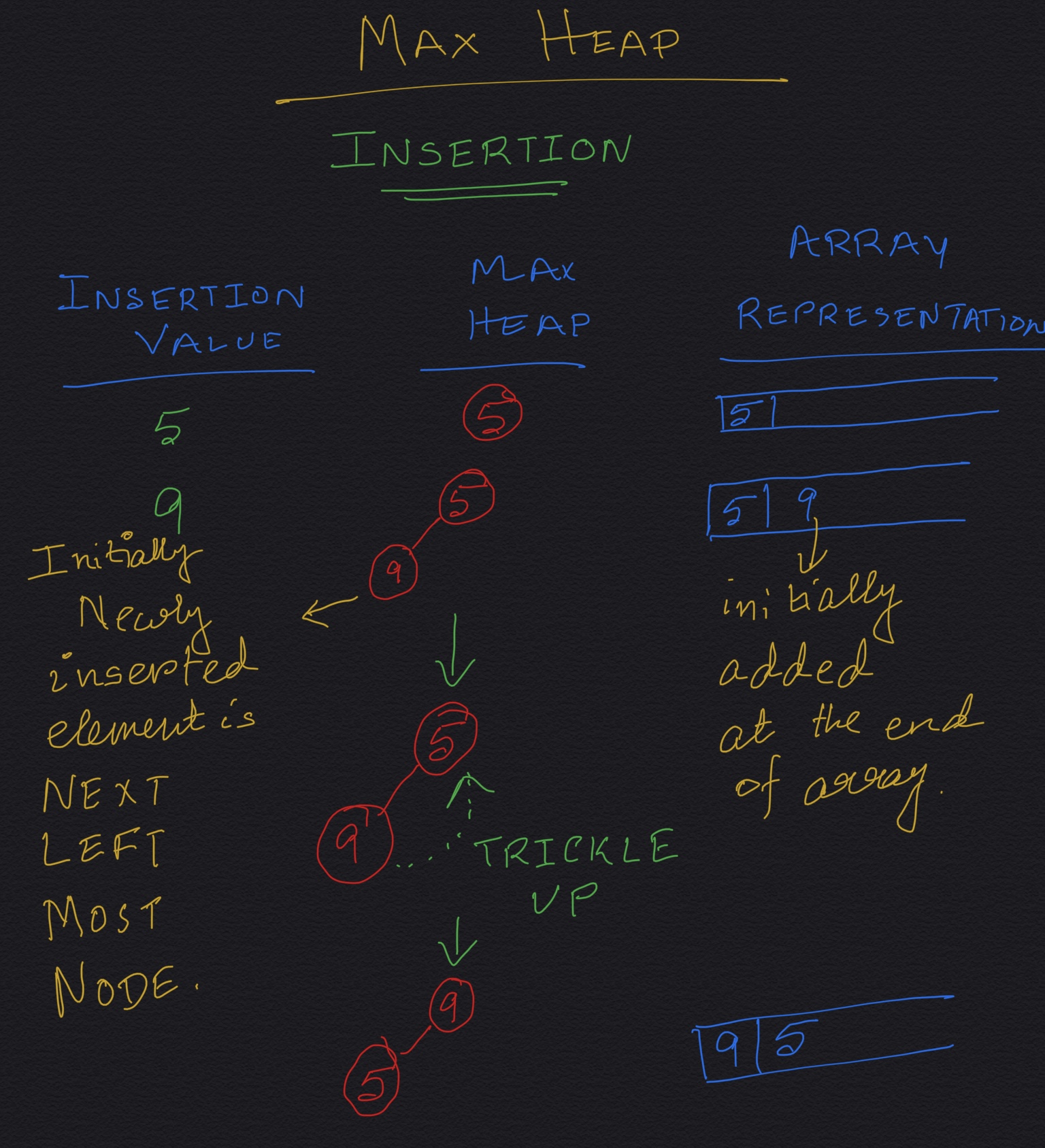
If the heap already has N elements, to begin with, we put the element at index N in the array (remember that the array is zero-based indexed). So, the new element becomes the last element in the array, initially. This means, if you think from the Complete Binary Tree perspective, the new element initially goes to the left-most available spot in the bottom-most level of the Complete Binary Tree. If the bottom-most level is already full, then we add a new level (new bottom-most level) in the Complete Binary Tree and the new element becomes the left-most element in the new next level.
Now we need to make sure that the addition of the new element is not violating the Heap Invariant: In Max Heap value of every node should be greater than the values of both its child nodes.
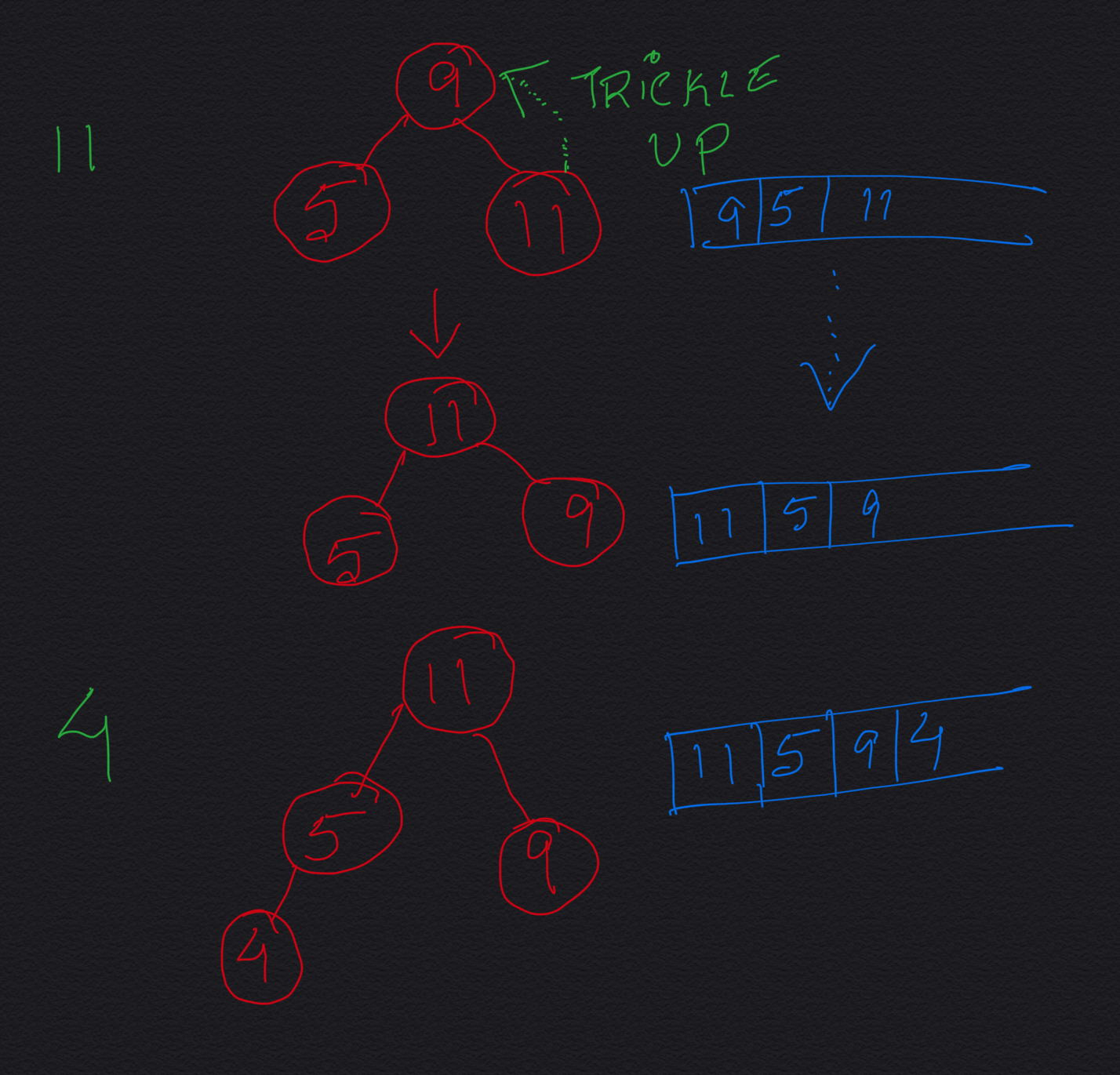
Trickle up: If the value of the new element is less than its current parent, we swap the places of the new element and its current parent. We go on doing this till the heap invariant is maintained again. If you notice, in this process the new element is going up. This process is called Trickle Up.
public void insert(int elem) throws Exception {
if (currentIndex > maxsize - 1) {
throw new Exception("Heap size has exceeded the maximum size. Cannot insert the element.");
}
arr[currentIndex] = elem;
trickleUp(currentIndex++); //the element is inserted at the last of the array. Now it should be
//trickled up unless the heap meets the heapify rule
}
private void trickleUp(int index) {
int parent = (index - 1) / 2;
while (index > 0 && arr[parent] < arr[index]) { //index > 0 because if the index ZERO
//then no need to trickle up as it is the root, so can't go any further up
swap(arr, index, parent);
index = parent;
parent = (parent - 1) / 2;
}
}
private void swap(int[] arr, int child, int parent) {
int temp = arr[child];
arr[child] = arr[parent];
arr[parent] = temp;
}
Delete Max:
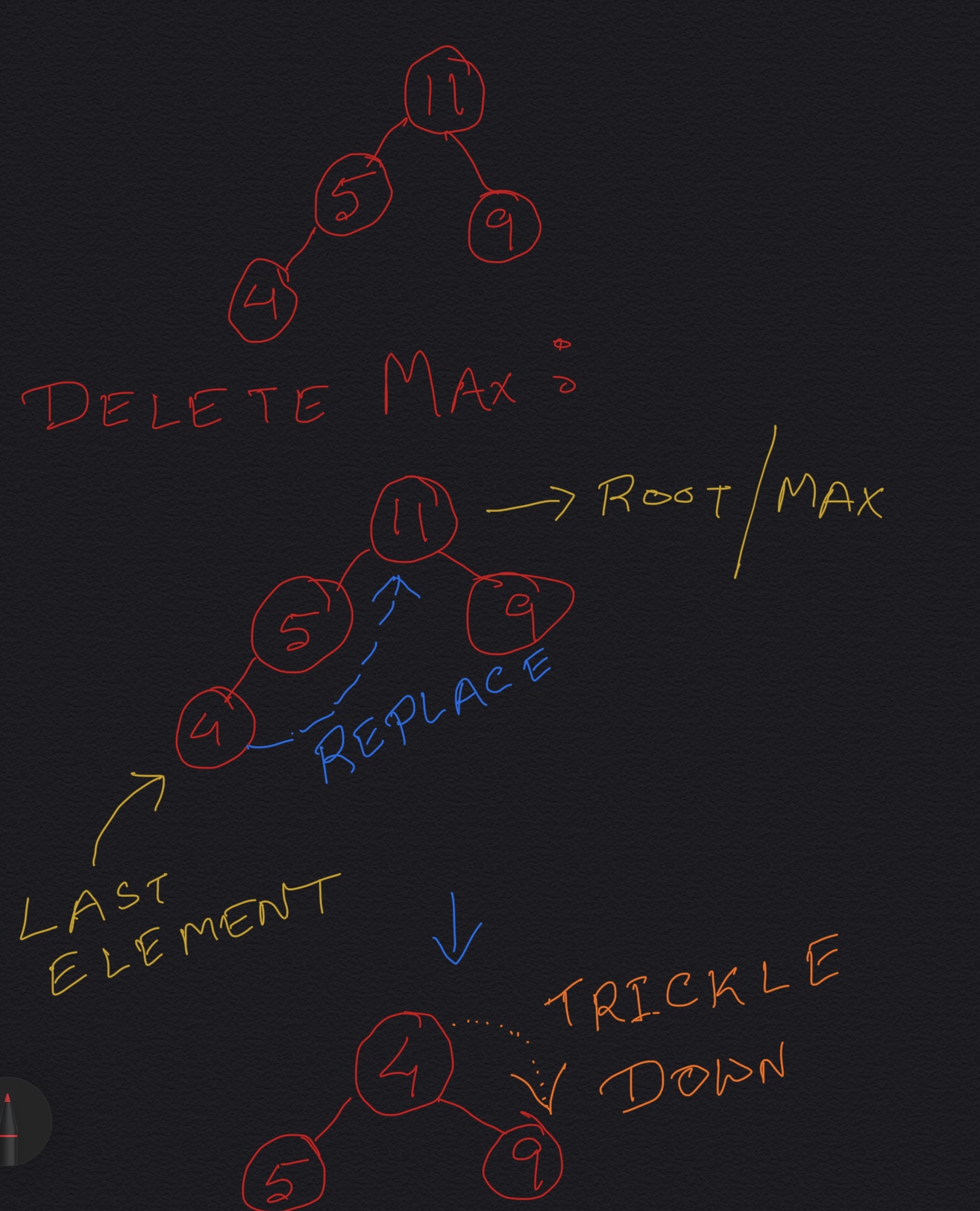
We know that the max element is at the root for Max Heap, which means it is the first element in the array (element at index 0). Our objective here is to remove the first element of the array. Removing the first element creates a vacancy at index 0. So what we do here is: replace the first element with the last element of the array. But now there is a high chance that the heap does not maintain the heap property any more: the root of the max heap might be lesser in value than at least one of its children. So we need to fix this. To fix this, we do a Trickle Down operation as described below:
- Replace the root of the heap with the last element on the last level.
- Compare the new root with its children; if they are in the correct order, stop.
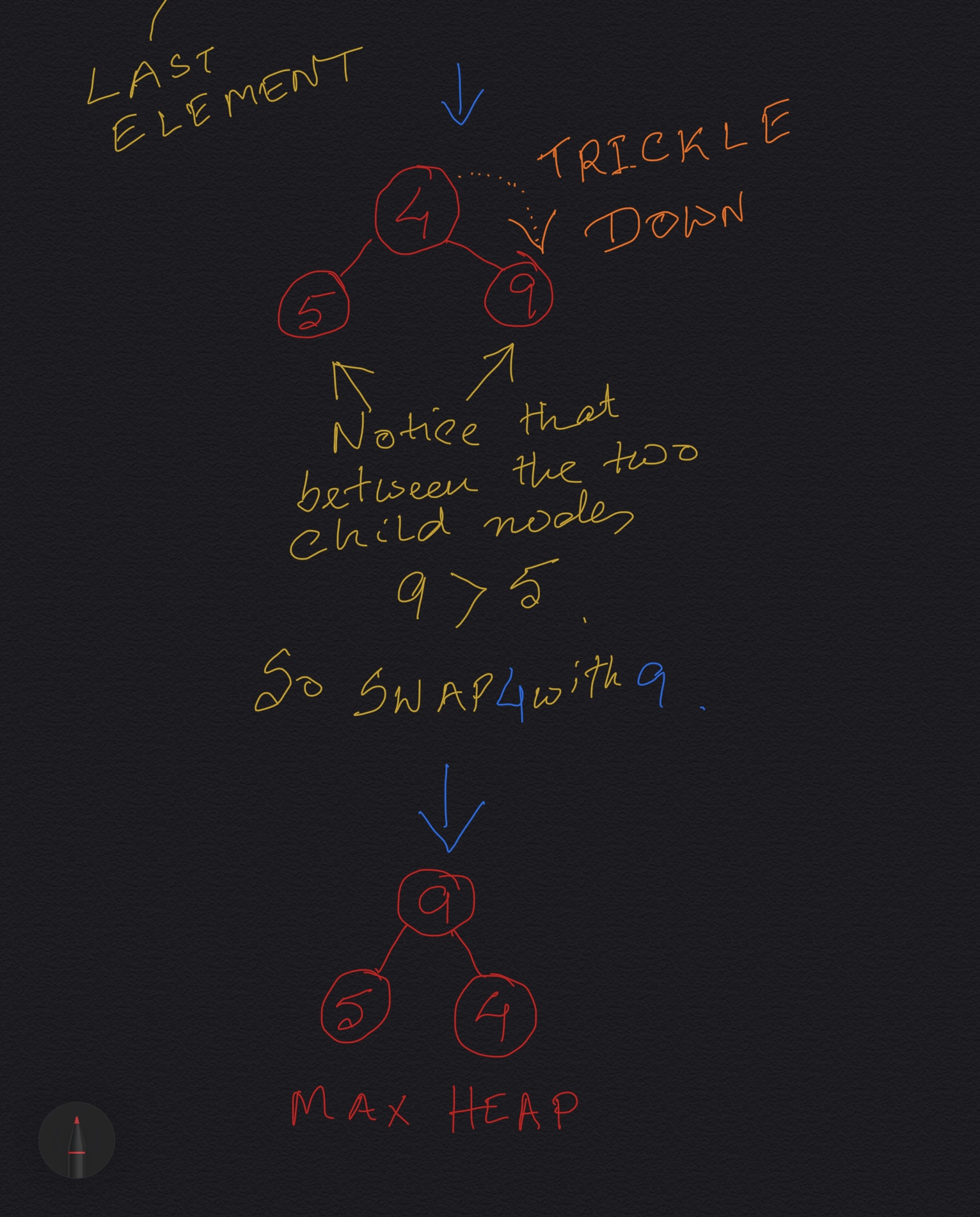
- If not, swap the element with the child which has larger value between two children and return to the previous step. (Swap with its smaller child in a min-heap).
public void removeMax() throws Exception {
if (currentIndex == 0) {
throw new Exception("There is no element in the heap.");
}
int last = arr[currentindex--]; //don't forget to decrement the currentIndex as we now
//have one less element after the removal
arr[0] = last; //in the removal procedure, the root i.e the max is removed and it is replaced
//by the last element and then it is trickled down till the heapify rule is maintained
trickleDown(0);
}
private void trickleDown(int index) {
while (index < (currentIndex / 2)) { //currentIndex used, NOT maxsize,
//because currently only currentIndex number of nodes are there
int child1 = (index * 2) + 1;
int child2 = (index * 2) + 2;
int largest = index;
if (child1 < currentIndex && arr[index] < arr[child1]) {
largest = child1;
}
if (child2 < currentIndex && arr[largest] < arr[child2]) {
largest = child2;
}
if (largest == index) {
break;
} else {
swap(arr, largest, index);
index = largest;
}
} // end of while
}
Complete Code:
Login to Access Content
Time Complexity:
-
getMax():
O(1)
-
Insertion:
In worst case, the time complexity is O(height of the heap), since we might have to do trickleUp operation from the leaf level to all the way up to the root. In worst case, the newly added value happens to be the largest value so far in the max heap and consequently becomes the new root. height = log2N, where N = total number of elements in the heap. So, time complexity = O(log2N).
-
Delete Max:
In worst case, the time complexity is O(height of the heap), since we might have to do trickleDown operation from the root level to all the way down to the leaf level.
height = log2N, where N = total number of elements in the heap. So, time complexity = O(log2N).
Now that you have a very good idea about how heap works, here is a cool app you could play around with: https://www.cs.usfca.edu/~galles/visualization/Heap.html.
