

Depth First Search or DFS
Get started
জয় শ্রী রাম
🕉Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
The below gif illustrates graphically how vertices in a graph are discovered in Depth First Search:
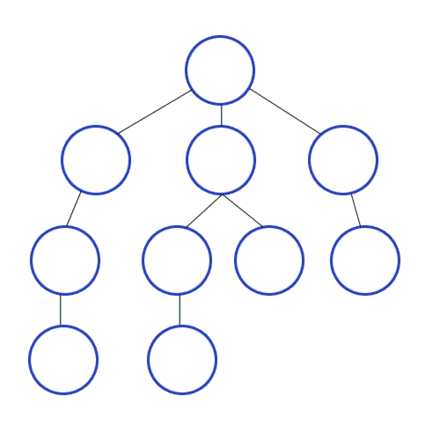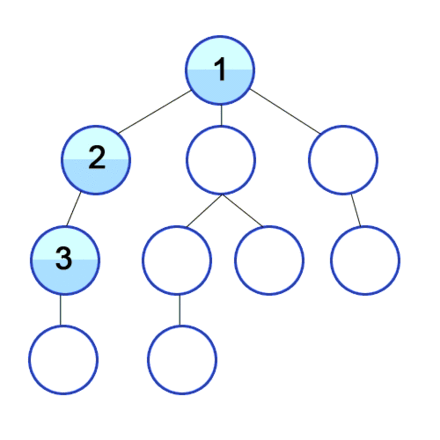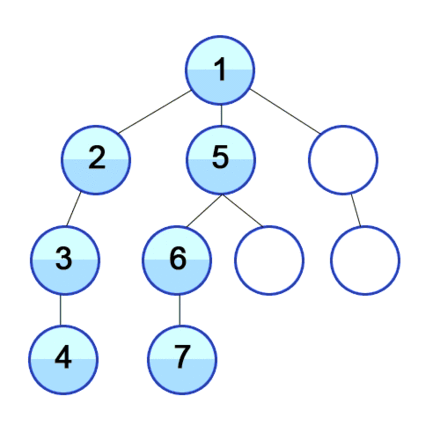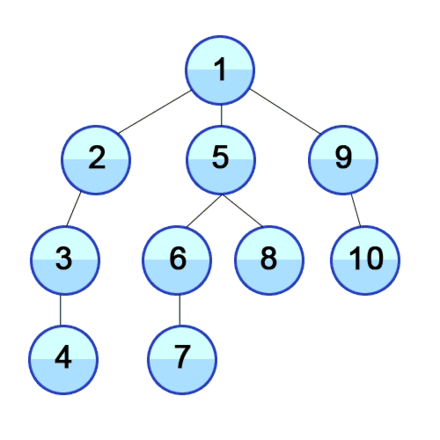
The DFS algorithm is a recursive algorithm that uses the idea of backtracking. It involves exhaustive searches of all the nodes by going ahead, if possible, else by backtracking.
Backtrack means that when you are moving forward and there are no more nodes along the current path, you move backwards on the same path to find nodes to traverse. All the nodes will be visited on the current path till all the unvisited nodes have been traversed after which the next path will be selected.
While implementing DFS it is important to ensure that the nodes that are visited are marked. This will prevent us from visiting the same node more than once if there is one or more cycle(s). If we do not mark the nodes that are visited and we visit the same node more than once, we may end up in an infinite loop.
Pseudocode:
DFS-recursive(G, s):
mark s as visited
for all neighbors w of s in Graph G:
if w is not visited:
DFS-recursive(G, w)
Code Implementation:
Java code:
import java.util.*;
/**
* Created by Abhishek on 4/12/21.
*/
public class DFS {
// prints all not yet visited vertices reachable from s
private List<Integer> DFS(int root, Map<Integer, List<Integer>> adjacencyLists, Set<Integer> visited, List<Integer> res)
{
visited.add(root); // mark discovered node as visited, to avoid infinite loop if there is one or more cycle(s)
// Process:
// process the node here if you want to process the node before processing
// all the nodes in the subgraph rooted at this node (i.e, before all the nodes that would be discovered
// after this node). This is similar to concept of PREORDER Traversal .
//
// Remember processing varies from problem to problem depending on the problem statement.
// For our basic DFS we just need to put the node in the list res.
res.add(root);
for (int adjacentNode : adjacencyLists.get(root)) {
if (!visited.contains(adjacentNode)) {
DFS(adjacentNode, adjacencyLists, visited, res); // do DFS on unvisited adjacent nodes
}
}
// Process:
// process the node here instead, if you want to process the node after processing
// all the nodes in the subgraph rooted at this node (i.e, after all the nodes that were discovered
// after this node). This is similar to concept of POSTORDER Traversal .
//
// Remember processing varies from problem to problem depending on the problem statement.
// For our basic DFS we just need to put the node in the list res.
//
// Just for your knowledge: If you want to implement this (processing a node after processing all the
// nodes in the sub-graph rooted at the node) ITERATIVELY, it would be bit harder than implementing recursively.
// More on this later.
// res.add(root);
return res;
}
// prints all vertices in DFS manner
public void performDFS(Map<Integer, List<Integer>> adjacencyLists)
{
Set<Integer> visited = new HashSet<>();
List<Integer> res = new ArrayList<>();
for (int node : adjacencyLists.keySet()) {
if (!visited.contains(node)) {
DFS(node, adjacencyLists, visited, res);
}
}
for (int node : res) {
System.out.print(node + " ");
}
}
public static void main(String[] args) {
Map<Integer, List<Integer>> graph = new HashMap<>();
/*
1 8
/ \
2 -- 3 -----
/ \ \ \
4 -- 5 6 -- 7
*/
graph.put(1, new ArrayList<Integer>(){{ add(2); add(3); }});
graph.put(2, new ArrayList<Integer>(){{ add(3); add(4); add(5); }});
graph.put(3, new ArrayList<Integer>(){{ add(6); add(7); }});
graph.put(4, new ArrayList<Integer>(){{ add(2); add(5); }});
graph.put(5, new ArrayList<Integer>(){{ add(2); add(4); }});
graph.put(6, new ArrayList<Integer>(){{ add(3); add(7); }});
graph.put(7, new ArrayList<Integer>(){{ add(3); add(6); }});
graph.put(8, new ArrayList<>());
DFS ob = new DFS();
ob.performDFS(graph);
}
}
Python Code:
Login to Access Content
Iterative Implementation:
This recursive nature of DFS can be implemented using stacks. The basic idea is as follows:
- Pick a starting node and push all its adjacent nodes into a stack.
- Pop a node from stack to select the next node to visit and push all its adjacent nodes into a stack.
- Repeat this process until the stack is empty. However, ensure that the nodes that are visited are marked. This will prevent you from visiting the same node more than once. If you do not mark the nodes that are visited and you visit the same node more than once, you may end up in an infinite loop.
Pseudocode:
DFS-iterative (G, s): //Where G is graph and s is source vertex
let S be stack
S.push( s ) //Inserting s in stack
mark s as visited.
while ( S is not empty):
//Pop a vertex from stack to visit next
v = S.pop( )
//Push all the neighbours of v in stack that are not visited
for all neighbours w of v in Graph G:
if w is not visited :
S.push( w )
mark w as visited
Code Implementation:
Java code:
import java.util.*;
/**
* Created by Abhishek on 4/12/21.
*/
public class DFS {
public static void main(String[] args) {
Map<Integer, List<Integer>> graph = new HashMap<>();
/*
1 8
/ \
2 -- 3 -----
/ \ \ \
4 -- 5 6 -- 7
*/
graph.put(1, new ArrayList<Integer>(){{ add(2); add(3); }});
graph.put(2, new ArrayList<Integer>(){{ add(3); add(4); add(5); }});
graph.put(3, new ArrayList<Integer>(){{ add(6); add(7); }});
graph.put(4, new ArrayList<Integer>(){{ add(2); add(5); }});
graph.put(5, new ArrayList<Integer>(){{ add(2); add(4); }});
graph.put(6, new ArrayList<Integer>(){{ add(3); add(7); }});
graph.put(7, new ArrayList<Integer>(){{ add(3); add(6); }});
graph.put(8, new ArrayList<>());
DFS ob = new DFS();
ob.performDFS_iterative(graph);
}
public void performDFS_iterative(Map<Integer, List<Integer>> adjacencyLists)
{
Set<Integer> visited = new HashSet<>();
List<Integer> res = new ArrayList<>();
for (int node : adjacencyLists.keySet()) {
if (!visited.contains(node)) {
DFS_iterative(node, adjacencyLists, visited, res);
}
}
for (int node : res) {
System.out.print(node + " ");
}
}
private List<Integer> DFS_iterative(int root, Map<Integer, List<Integer>> adjacencyLists, Set<Integer> visited, List<Integer> res)
{
Stack<Integer> stack = new Stack<>();
stack.push(root);
visited.add(root);
while (!stack.isEmpty()) {
int curr = stack.pop();
res.add(curr); // Process current vertex in PREORDER manner
for (Integer adjacentNode : adjacencyLists.get(curr)) {
if (!visited.contains(adjacentNode)) {
visited.add(adjacentNode);
stack.push(adjacentNode);
}
}
}
return res;
}
}
Python Code:
Login to Access Content
If you have a requirement to implement DFS in
POSTORDER manner, implementing iteratively might not be as trivial as
implementing recursively. Please take a look at
Iterative Postorder Traversal with Single Stack.
-
I often get this question:
What are some types of problems that are much harder to solve in iterative DFS rather than recursive DFS ?
Answer: Any problem requiring you to process the current node after finishing DFS on all unvisited nodes in sub-graph rooted at the current node (like, Postorder Traversal) would be, in most cases, harder to implement a solution using iterative DFS as compared to recursive DFS. Take a look at how non-trivial it is to implement Iterative Postorder Traversal as compared to how easy it is to implement Iterative Preorder Traversal.
Time Complexity:
The best way to compute the time complexity would be to think about how many nodes you are processing and how many time you ar processing each nodes. For example, If in our code a node is not visited more than once then a DFS operation would be O(n).As for the |E| part, |E| which represents total number of edges present in the graph, will ultimately be expressed in terms of number of nodes (|V| or n). It depends on whether the graph is dense or sparse. If a graph is dense in most cases you would see that
|E| = |V|*|V| = n ^ 2 .
It would also depend whether you are representing the graph using Adjacency List or Adjacency Matrix and the way you are implementing them.
To give a very general idea:
In DFS, you traverse each node exactly once. Therefore, the time complexity of DFS is at least O(V).
Now, any additional complexity comes from how you discover all the outgoing paths or edges for each node which, in turn, is dependent on the way your graph is implemented. If an edge leads you to a node that has already been traversed, you skip it and check the next. Typical DFS implementations use a hash table to maintain the list of traversed nodes so that you could find out if a node has been encountered before in O(1) time (constant time).
-
If your graph is implemented as an adjacency matrix (a V x V array), then,
for each node, you have to traverse an entire row of length V in the
matrix to discover all its outgoing edges.
Please note that each row in an adjacency matrix corresponds
to a node in the graph, and the said row stores information
about edges stemming from the node. So, the complexity of
DFS is O(V * V) = O(V^2).
-
If your graph is implemented using adjacency lists, wherein each node maintains a list of all its adjacent edges, then, for each node, you could discover all its neighbors by traversing its adjacency list just once in linear time. For a directed graph, the sum of the sizes of the adjacency lists of all the nodes is E (total number of edges). So, the complexity of DFS is O(V) + O(E) = O(V + E).
- For an undirected graph, each edge will appear twice in the adjacency list: for an edge AB, A would appear in adjacency list of B, and B would appear in adjacency list of A. So, the overall complexity will be O(V) + O (2E) ~ O(V + E).
Space Complexity:
DFS goes along a path all the way down before it backtracks and store all the nodes in the path in the recursion stack. So, the size of the stack would grow as large as the height of the longest path. The space complexity for DFS is O(h) where h is the maximum height of the tree.
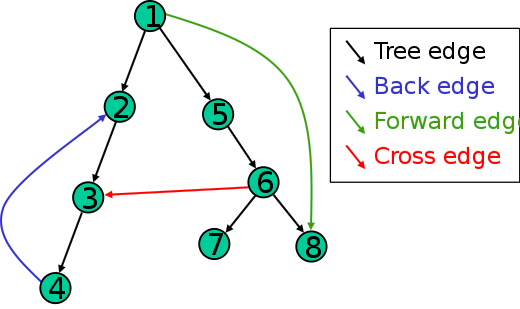
DFS Edges:
A DFS tree is a spanning tree. A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges.Based on this spanning tree, the edges of the original graph can be divided into four classes:
-
forward edges: edges which point from a node of the tree to one of its descendants,
-
back edges: edges which point from a node to one of its ancestors.
Concept of back edges has direct used in detecting cycles using DFS.
-
cross edges: edges which connects two node such that they do not have any ancestor and a descendant relationship between them.
-
tree edges: edges which are present in the tree obtained after applying DFS on the graph.
DFS is a versatile search method which has uses in a lot of various domains. Look at below chapters to see some of its amazing applications:
- Topological Sort
- Cycle Detection Using DFS
- All Paths Between Two Nodes
- Bipartite Graph
- Connected Components
- Articulation Points
- Finding Bridges
- Strongly Connected Components (SCC)
Now let's look at a non-trivial problem below and see how we use DFS in solving it. Computing the time complexity for this problem would be really fun!
Problem Statement:
Given a dictionary and a square (n x n) matrix of characters identify all the valid words that can be formed from adjacent characters in the matrix.
A P E R
T C A P
G E R M
G U M E
Some examples of valid words: APE, CAP, REAR, GEAR, PEAR, MAP, RACE, PACT
Solution:
To get all the words that can be formed from the matrix maintaining the condition described in the problem statement, we can do DFS starting from each cell in the matrix. In the Trie with DFS we will optimize it to start the DFS only from those cells which has character which can be a starting character in a a valid word. If we see the dictionary has no word with the starting character same as the character of the current cell then we should not waste time doing DFS from that cell.As we reach each cell as part of DFS we should see that the word formed till now is present in the dictionary. If yes, we add the word the word in the result list. Cycle must be avoided while doing DFS for each cell.
Java:
// One interesting part of this problem is to figure out what data structure to use for dictionary.
// We have quite a few choice for dictionary:
// 1. A not-so-good choice would be List, but time complexity for
// checking if a word is present in the dictionary would be O(m), where m is the total number of words in the dictionary.
//
// 2. HashSet : Average time complexity to search a word would be O(1), but in worst case
// the time complexity could be O(m) if there are too many collisions. Developers often rely on string hashcode
// but we need to keep in mind that string hashcode is 32 bit integer. For a string long enough for which hashcode overflows,
// since overflown part of the integer is lost and the rest is retained, there would be chances of collision.
// for your information, in Java "FB".hashCode() == "Ea".hashCode(), and each of them is equal to 2236.
//
// 3. Trie: which would be a perfect choice of data structure for our dictionary.
// Searching for a word in Trie would be O(k), where k is the length of the word being searched.
public Set<String> getAllValidWords(char[][] matrix, Set<String> dict) {
Set<String> res = new HashSet<>();
if (matrix == null || matrix.length == 0) {
return res;
}
int len = matrix.length;
StringBuilder sb = new StringBuilder();
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
int[][] visited = new int[len][len];
dfs(matrix, i, j, res, sb, visited, dict);
}
}
return res;
}
private void dfs(int[][] matrix, int row, int col, Set<String> res, StringBuilder sb, int[][] visited, Set<String> dict) {
int len = matrix.length;
if (row < 0 || col < 0 || row > len - 1 || col > len - 1 || visited[row][col])) {
return;
}
sb.append(new String(matrix[row][col));
if (dict.contains(sb.toString())) {
res.add(sb.toString());
}
visited[row][col] = true;
dfs(matrix, row - 1, col - 1, res, sb));
dfs(matrix, row - 1, col, res, sb));
dfs(matrix, row - 1, col + 1, res, sb));
dfs(matrix, row, col + 1, res, sb));
dfs(matrix, row + 1, col + 1, res, sb));
dfs(matrix, row + 1, col, res, sb));
dfs(matrix, row + 1, col - 1, res, sb));
dfs(matrix, row, col - 1, res, sb));
sb.setLength(sb.length() - 1);
visited[row][col] = false;
}
Time Complexity: getAllValidWords() method has a O(n^2) for-loop. dfs() calls itself 8 times and each of these call recurses O(n^2) times. So the time complexity is exponential.
dfs() has a time complexity of O(8^(n^2)). (n ^ 2) is the total number of characters present in the matrix. If the matrix were of dimension (m X n) then we would have O(8^(m*n)).
Put in a different way, every dfs() call is calling itself 8 times (from each of the adjacent matrix cells), and each of these 8 calls again calls itself 8 times and for each call it happens O(total number of cells in the matrix) time since we make sure we do not revisit a cell visited as part of the current DFS path. So it is 8 * 8 * 8 *....*(n2 times) = 8 n2 .
So the overall time complexity is O(n2.8n2).
The ( 8n2 ) might seem little difficult to understand for the beginners, but if the rewrite the dfs() method in the following way it becomes easier to understand how we got the exponential time complexity.
Java:
private void dfs(int[][] matrix, int row, int col, Set<String> res, StringBuilder sb, int[][] visited, Set<String> dict) {
int len = matrix.length;
if (row < 0 || col < 0 || row > len - 1 || col > len - 1 || visited[row][col]) {
return;
}
sb.append(new String(matrix[row][col));
if (dict.contains(sb.toString())) {
res.add(sb.toString());
}
visited[row][col] = true;
int[][] directions = {
{-1,-1}, {-1,0}, {-1,1},
{0, -1}, {0, 1},
{1, -1}, {1, 0}, {1, 1}
};
for (int[] direction : directions){ // loops 8 times
dfs(matrix, row + direction[0], col + direction[1], res, sb);
}
sb.setLength(sb.legth() - 1);
visited[row][col] = false;
}
Advanced Level Problems with DFS based Solutions:
- How to Send Message to Entire Social Network
- Disconnected Network
- Critical Connection
- Minimal Vertices
- Course Scheduling
